Motivation

The challenge involves tracking a target particle and planning a path which brings the player into contact with the target at a particular time $t_f$.

Investigation

Trivial approach

The trivial solution is to simply command the particle to prosecute the target’s current position, without extrapolating its behavior into the future. We don’t consider this possibility further.

Naive approach

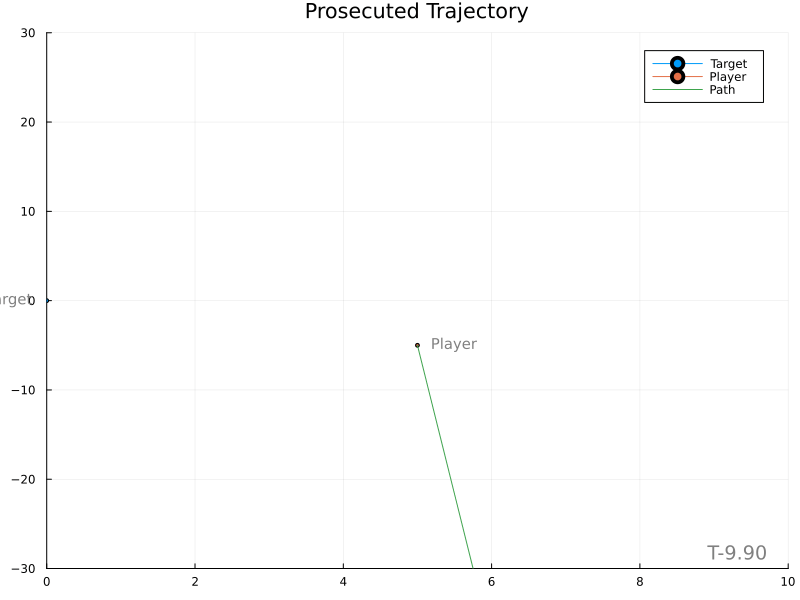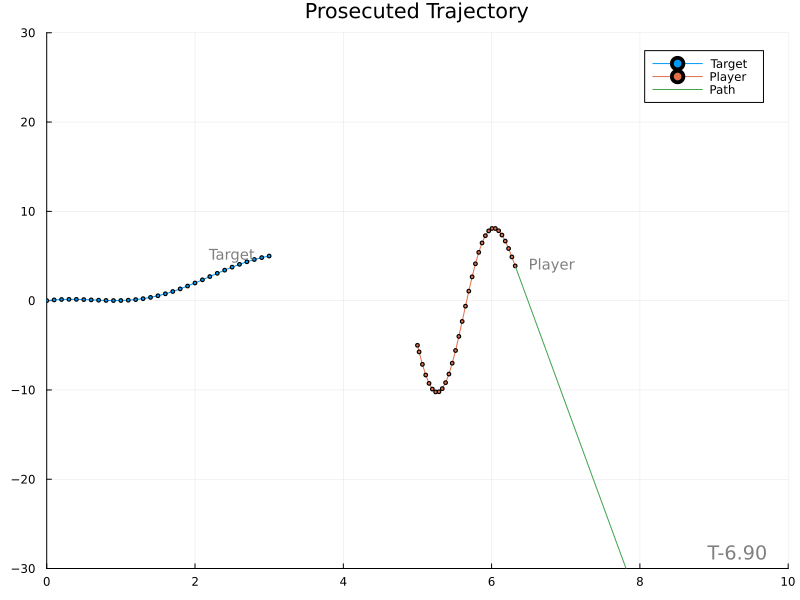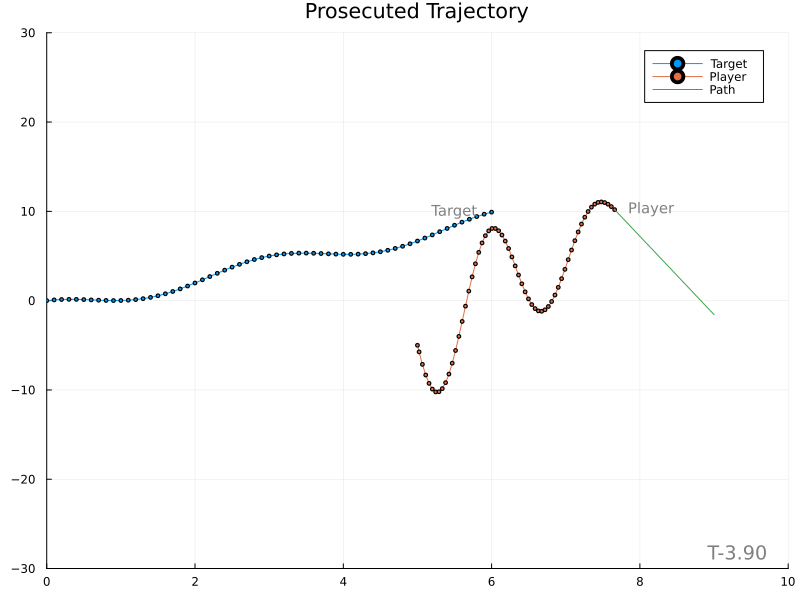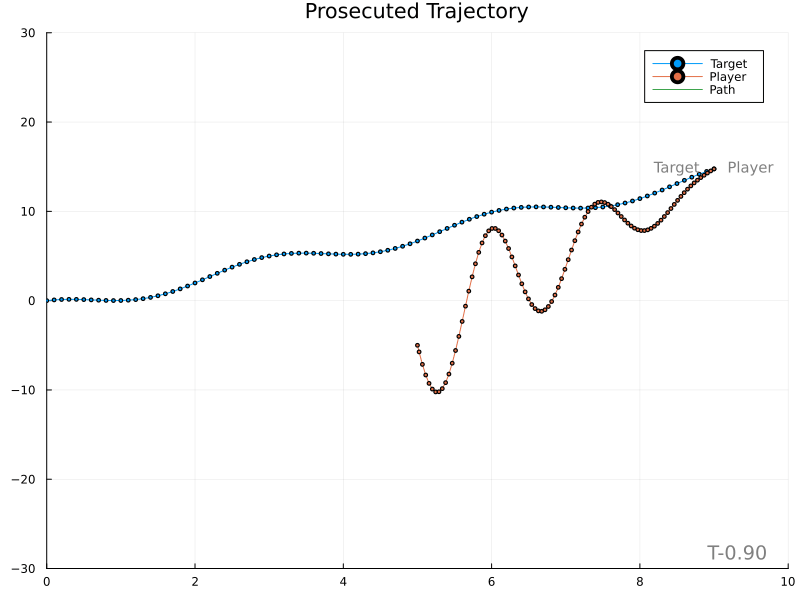
The next simplest solution is to predict the target’s position at the specified impact time and plan a direct course to that location. The impact location is found by integrating the target’s acceleration and using its current position and velocity as initial conditions. The speed of the player along its trajectory is equal to the distance it will travel divided by the impact time.

Results

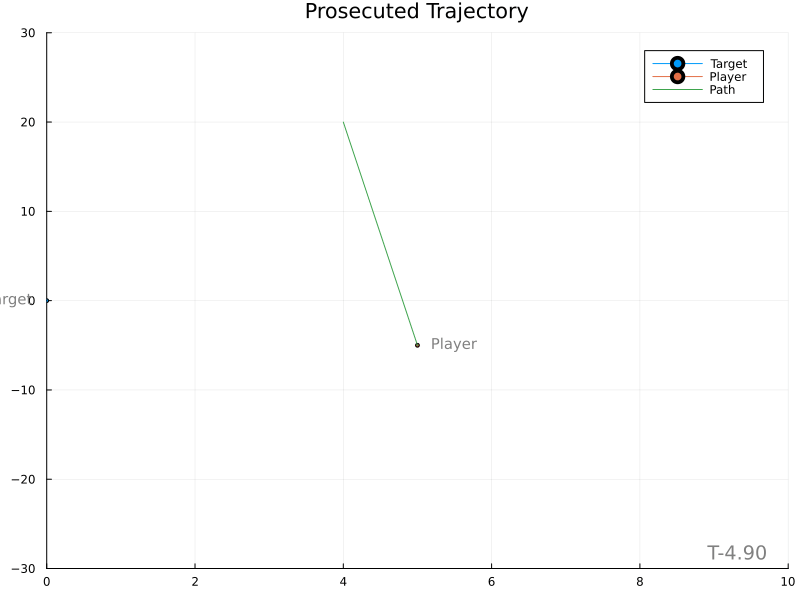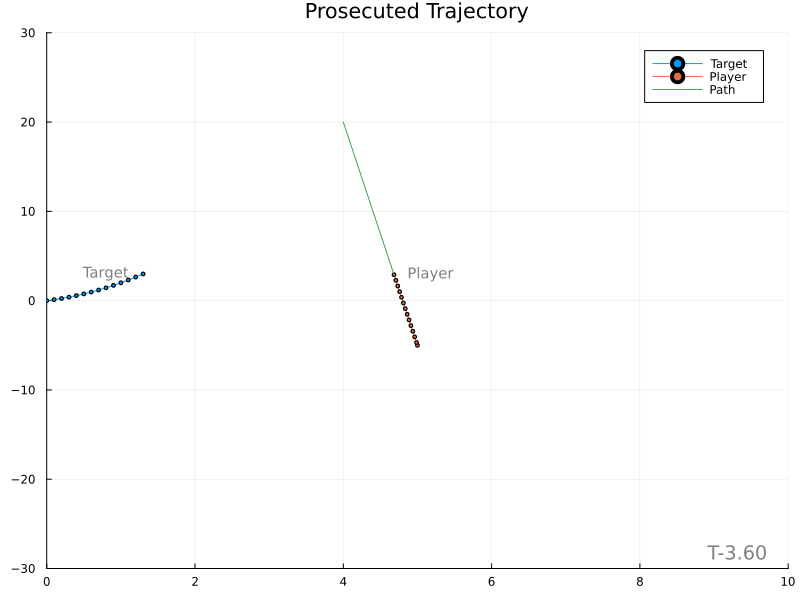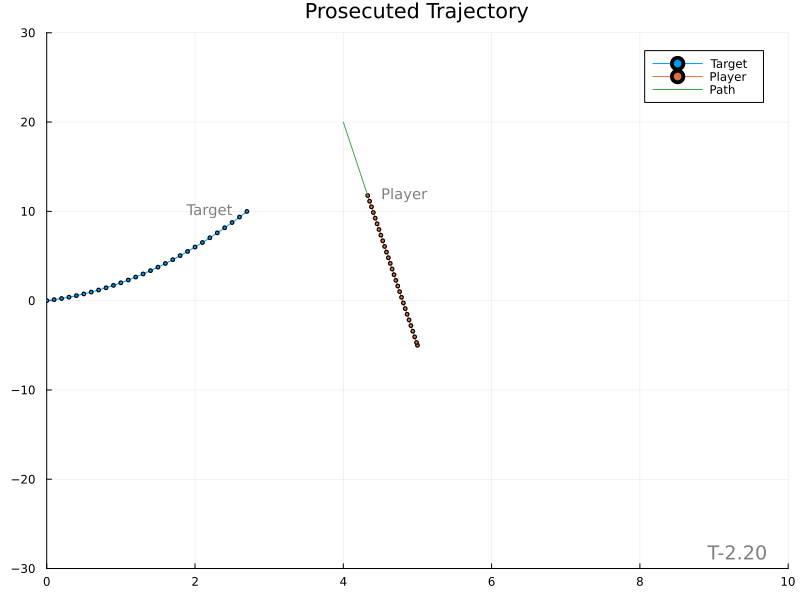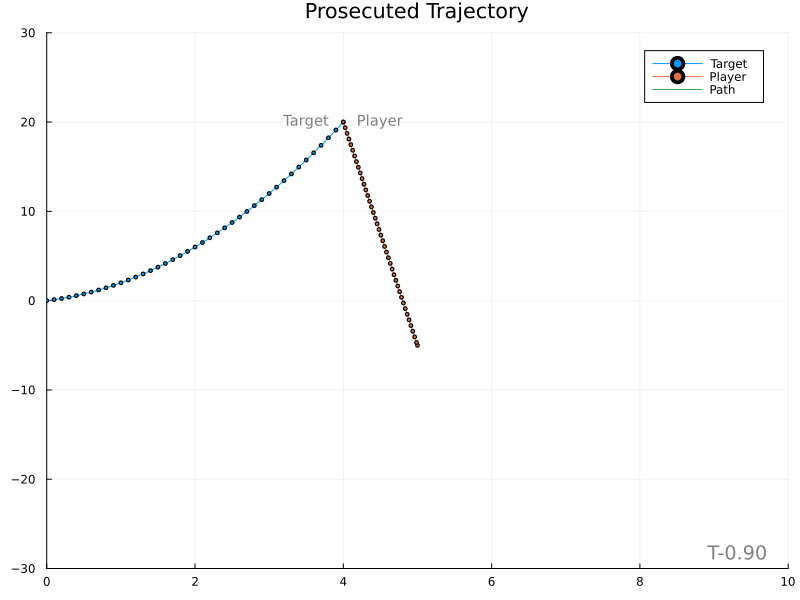
Matching target velocity

It is desirable to meet the target not only at a given position in space but also while traveling at its same velocity. This would be a “soft” catch instead of a hard collision.

To achieve this, a path is generated at every instant time which smoothly joints the player’s current position with the expected target location. The path is generated as a Bezier curve with end tangents defined by the player’s current velocity and the target’s expected velocity.

In path coordinates, the player’s speed must be a function of time. A linear model would suffice to meet strictly the target’s position; however, it offers insufficient degrees of freedom to reach the same position at a specified speed. A quadratic speed model would work.

\[\dot s(t) = a_2t^2 + a_1t + a_0\]

The three boundary conditions require:

1. The speed begin as equal to the player’s current speed

   \[\dot s(0) = v_0 = a_0\]

2. The speed end as equal to the expected target’s speed

   \[\dot s(t_f) = v_f = a_2t_f^2 + a_1t_f + a_0\]

3. The distance traveled by the player must be equal to the generated path’s length

   \[d = \int_0^{t_f} \dot s(t) dt = \frac{1}{3} a_2t_f^3 + \frac{1}{2} a_1t_f^2 + a_0t_f\]

Solving the system of linear equations yields:

\[a_2 = \frac{3(v_ft_f + v_0t_f - 2d)}{t_f^3} \\ a_1 = \frac{-2(v_ft_f + 2v_0t_f - 3d)}{t_f^2} \\ a_0 = v_0\]

The player speed at the next simulated time-step is found as $\dot s(dt)$. To calculate velocity, the tangent vector to the planned path at the next timestep is also required. First, $\dot s(t)$ is integrated over the timestep to find $ds$, the distance traveled along the path. The parameter which yields this point along the Bezier curve is worked numerically and used to obtain the tangent vector at the particle’s next timestep. The commanded acceleration is finally obtained as the difference between the player’s next and current velocity.

Results

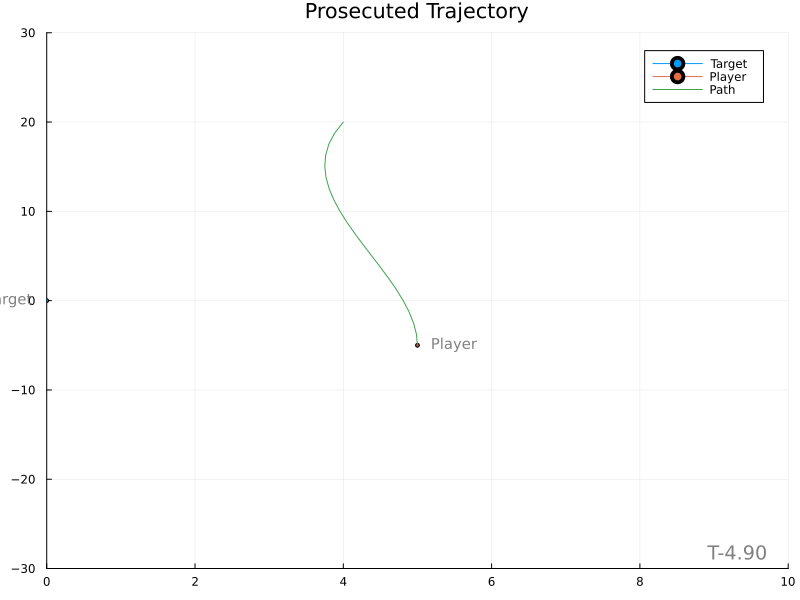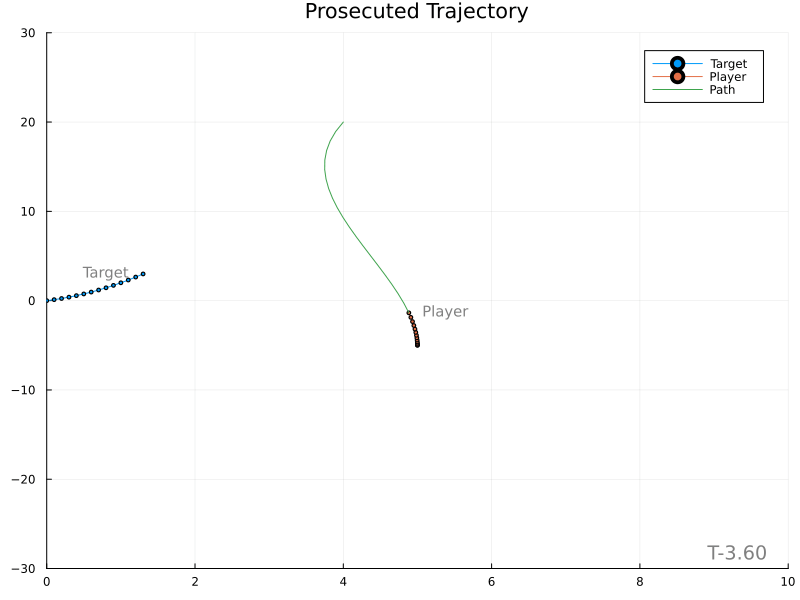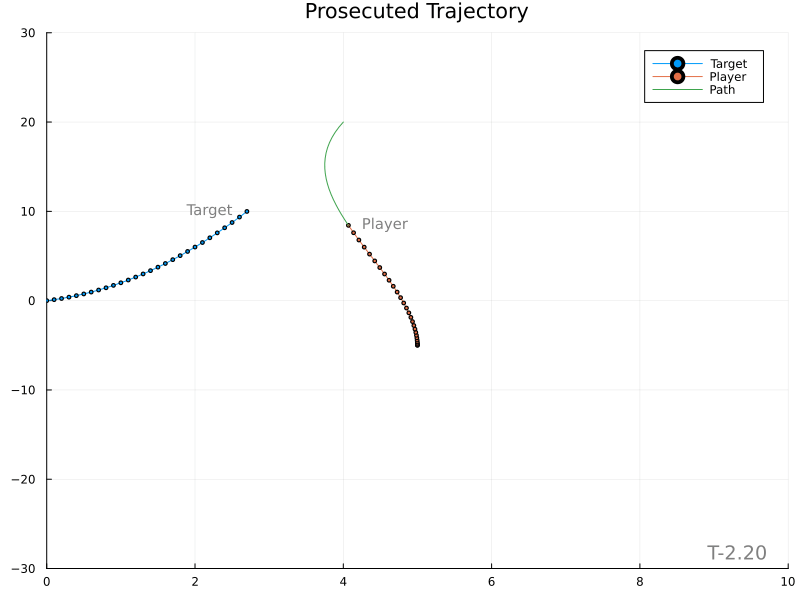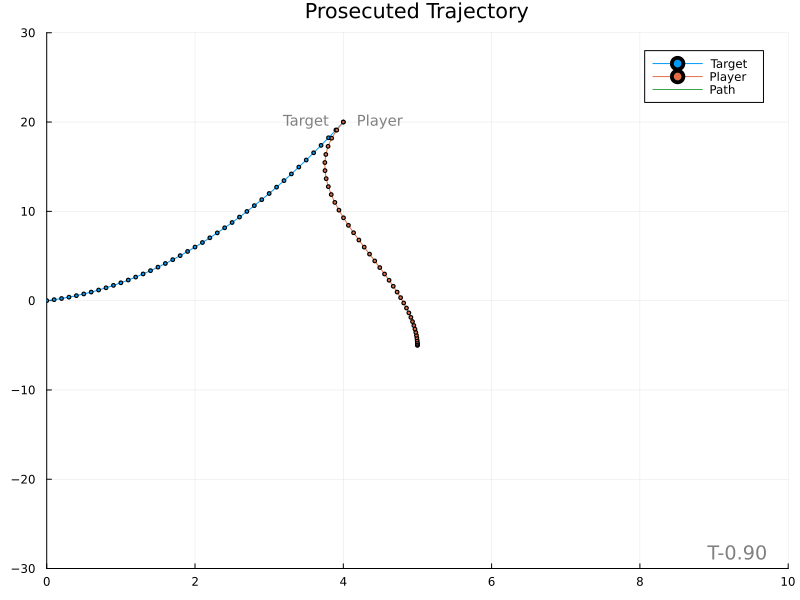
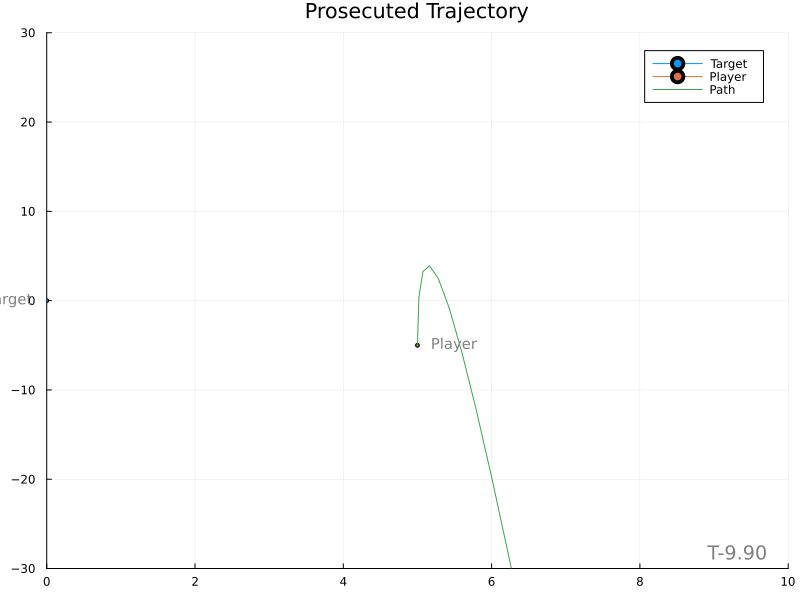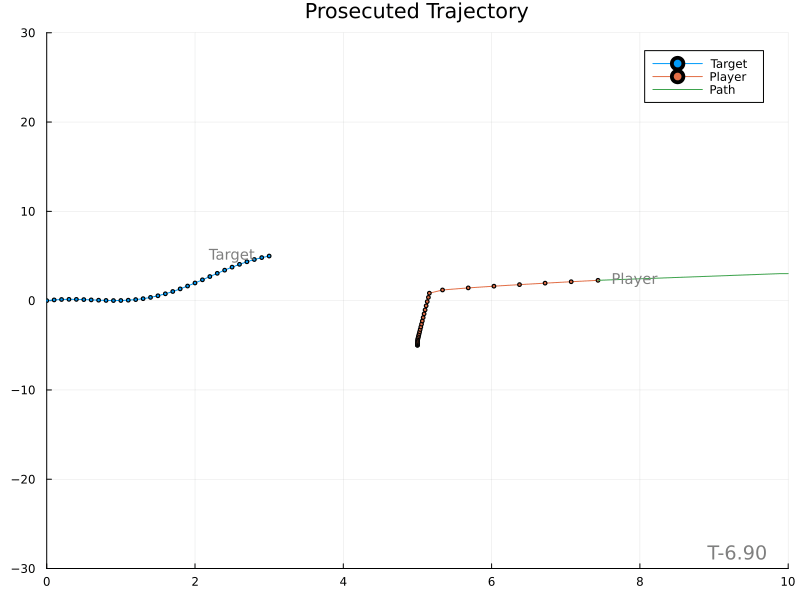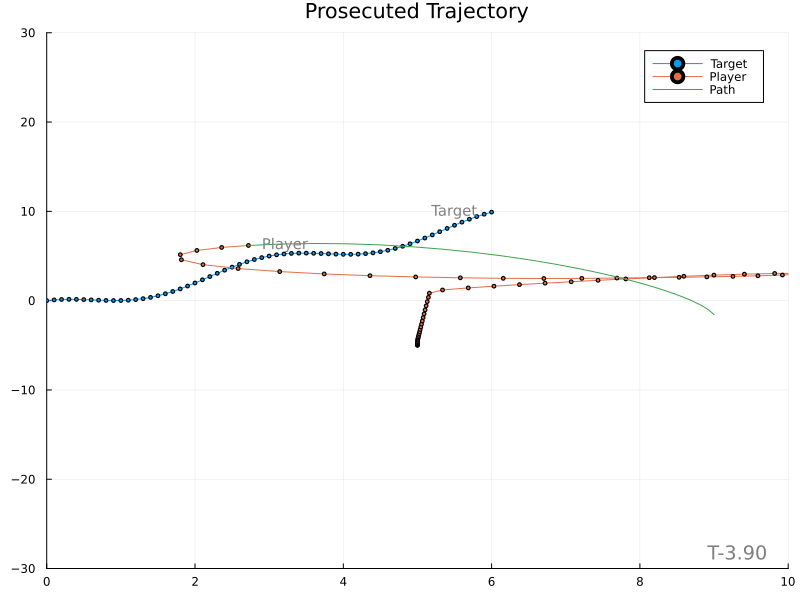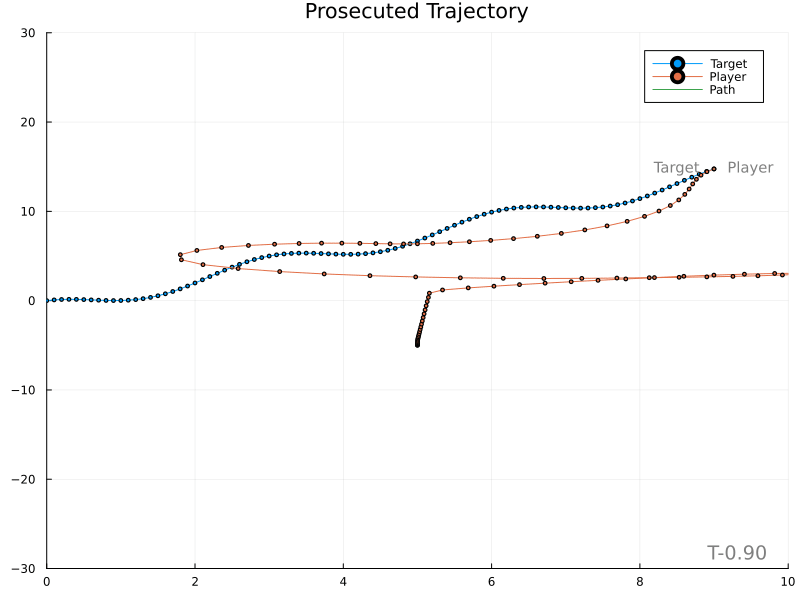
Unfortunately, it’s evident that variations in the target’s velocity cause large changes in the expected meet location, in turn producing rather wild player paths.

Applying a filter to tracked acceleration

When the player is further away from the target, it may make sense to filter rapid changes in the target’s behavior. Even small changes in acceleration extrapolate to large differences in the target’s future location; but if those changes are cyclic or noisy, the player ends up losing large amounts of energy by chasing a rapidly changing path.

To test this theory, a simple weight is applied to the target’s acceleration when predicting its location and impact time. The weight caps at 1.0 and limits to 0.0 when the player is infinitely far from the target.

Results

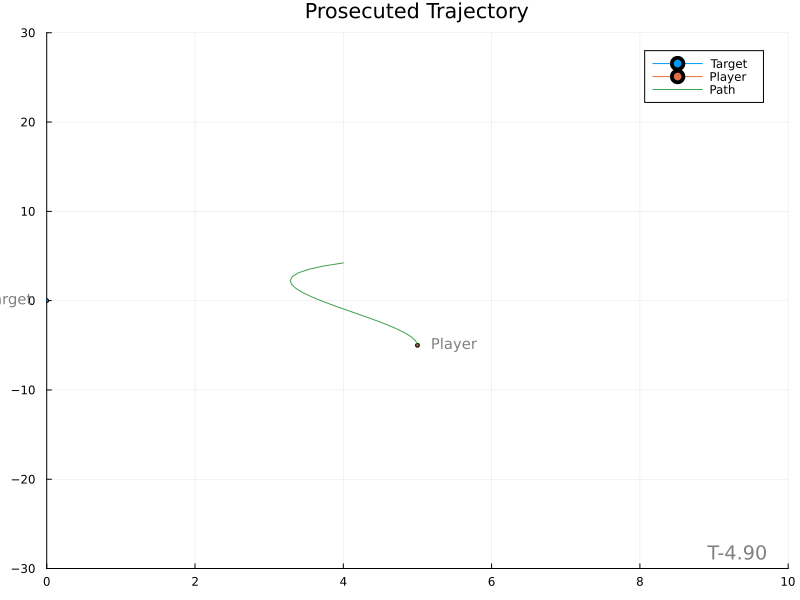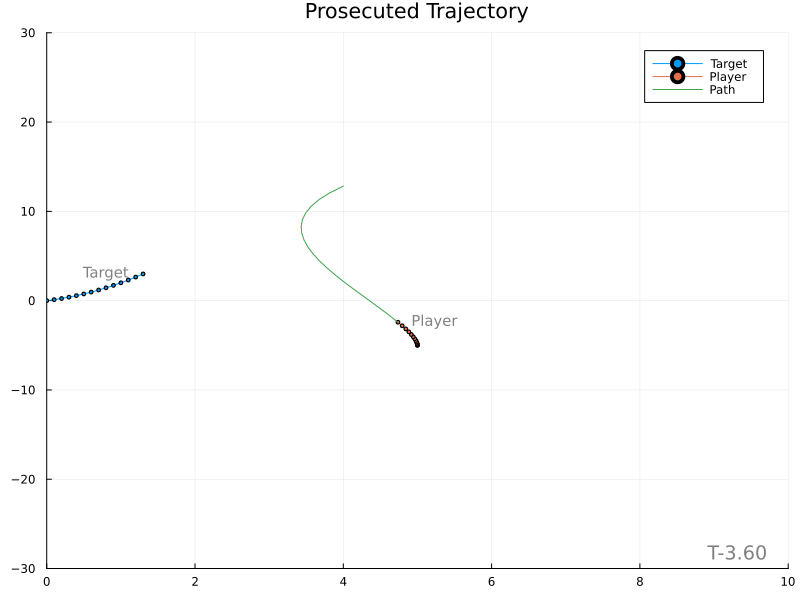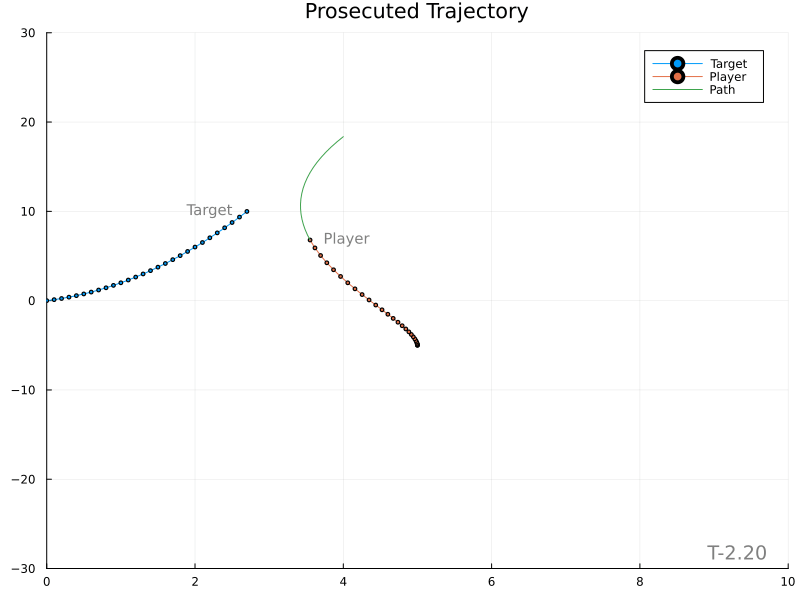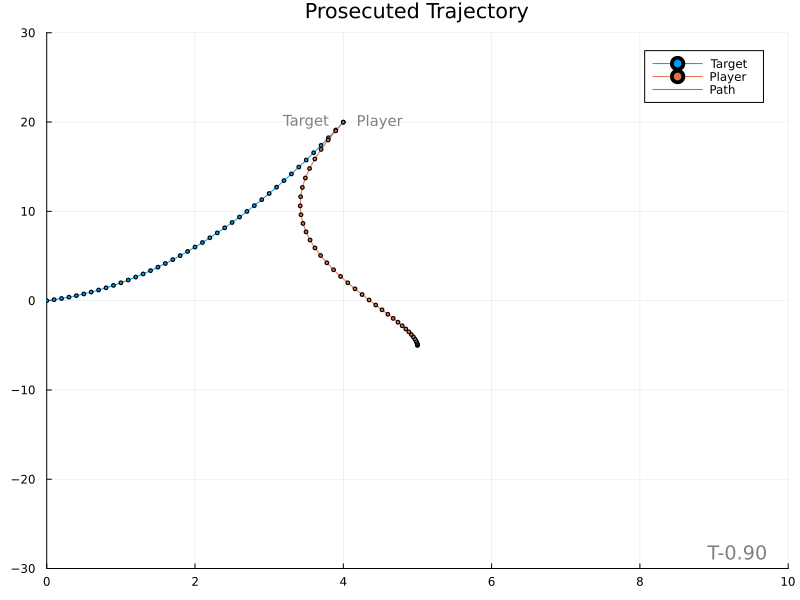
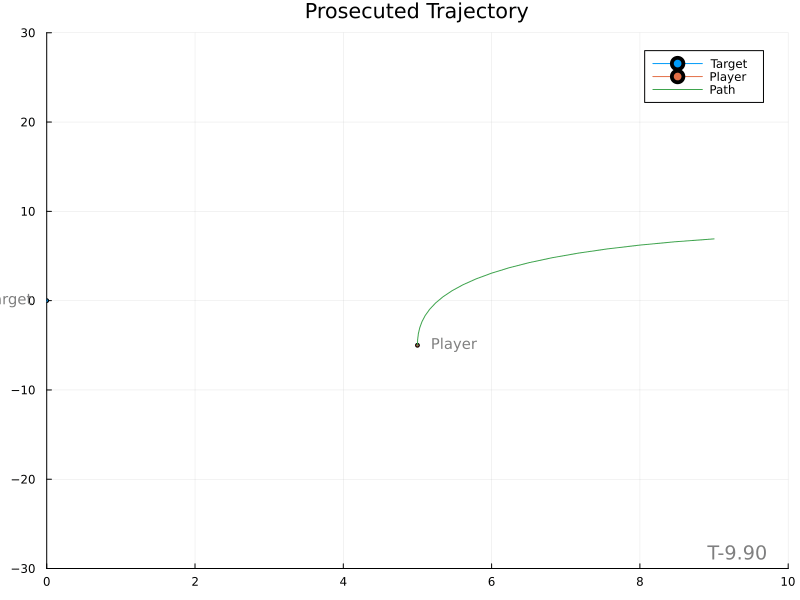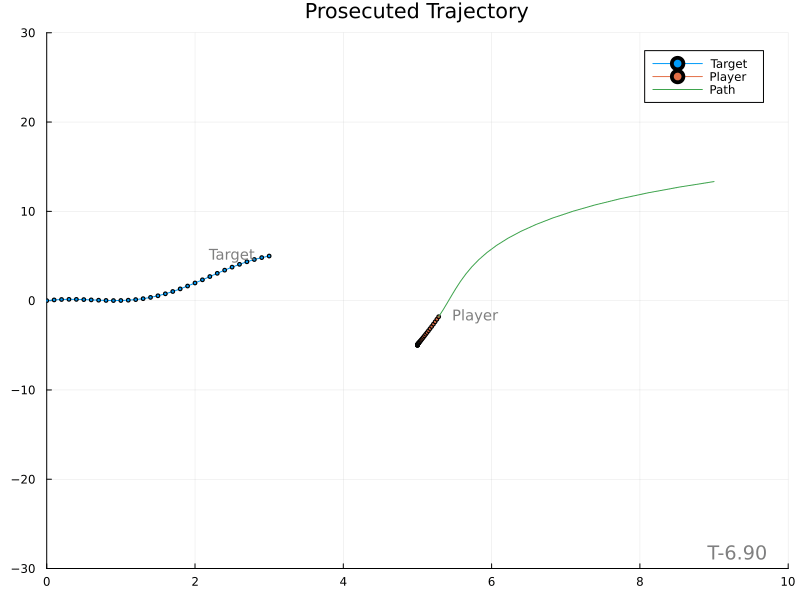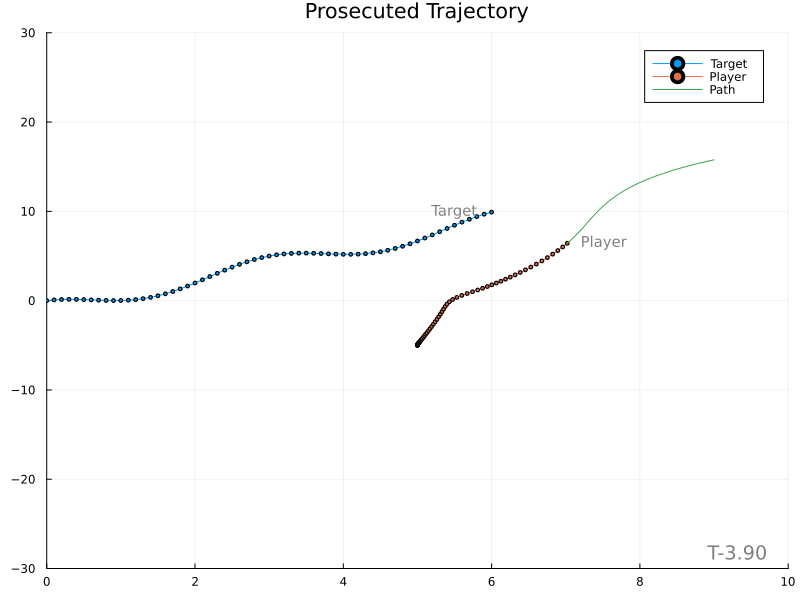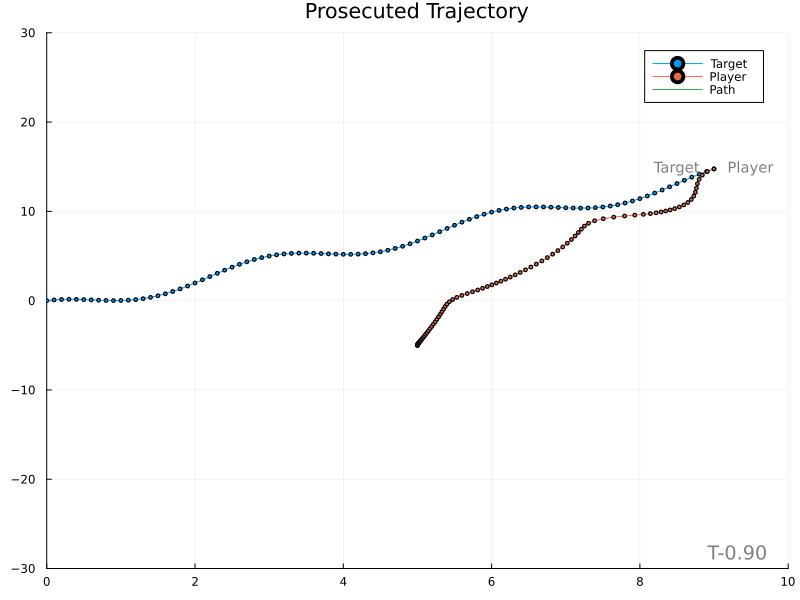
This is much better. The player still moves somewhat abruptly, leaving room for improvement. Use of a proper lowpass filter may introduce a “smoothing” lag and should be tried next.

Details

The plots are generated via a sandbox written in Julia. The main control loop is very simple:

for t in time_range
    # Stage the target
    p = Sinusoidal()
    stage_path!(p, target, t)

    # Control
    c = N1()
    path = controller!(c, target, player, impact_time - t, dt)
    push!(planned_paths, path)

    # Step particles
    move_particle!(target, dt)
    move_particle!(player, dt)
end

The particle types are simple objects:

struct Particle{T}
    id::Int64
    pos::Vector{Vector{T}}
    vel::Vector{Vector{T}}
    acl::Vector{Vector{T}}
    function Particle(id::Int64)
        new{Float64}(id, [fill(0.0, 3)], [fill(0.0, 3)], [fill(0.0, 3)])
    end
end

The target path is controlled by applying an acceleration:

abstract type Path end
struct Linear <: Path end
struct Quadratic <: Path end
struct Sinusoidal <: Path
    w::Float64
    m::Float64
    function Sinusoidal()
        new(2., 4.)
    end
end

function stage_path!(path::Linear, particle::Particle, t::Float64)
    particle.acl[end] = [0.0, 0.0, 0.0]
end

function stage_path!(path::Quadratic, particle::Particle, t::Float64)
    particle.acl[end] = [0.0, 2.0, 0.0]
end

function stage_path!(path::Sinusoidal, particle::Particle, t::Float64)
    particle.acl[end] = [0.0, -path.m*sin(path.w*t), 0.0]
end

While a sample controller commands player acceleration for the next timestep:

abstract type Controller end
struct N1 <: Controller end
struct N2 <: Controller end

# Based on standard position projection
function controller!(controller::N1, target::Particle, player::Particle, time2impact::Float64, dt::Float64)
    predicted_target_pos = project_particle_pos(target, time2impact)
    new_vel = (predicted_target_pos - player.pos[end]) / time2impact
    player.acl[end] = (new_vel - player.vel[end]) / dt

    # Return path points
    points = []
    for i in 0:0.05:1
        push!(points, player.pos[end] + i*(predicted_target_pos - player.pos[end]))
    end

    return points
end